
Eduard Template Squares STEEL
By Jacob Russell
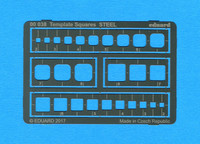
This photo etch set from Eduard is 2 sets of scribing templates for 2 types of squares with 2 different styles of rounded corners. It consists of a total of 26 template squares. You get 2 sets of 13 squares. The sets are divided into pairs of templates.
The 2 larger templates have 10 squares each, with each square approximately .25mm smaller than the previous one. Both sets of squares are the same size; the corner radius of one set is greater than the other. The smaller templates contain 3 squares each and these are simply the largest squares for each set.
I am a real fan of Eduard's scribing templates. Sometimes kits are missing key surface details like access hatches, so you can use these templates to add them. These templates are also indispensable for scratch building.
I recommend this set and I would like to thank Eduard for providing the review sample.
|
